Peluang (Probabilitas) adalah cabang matematika tentang deskripsi numerik tentang seberapa besar kemungkinan suatu peristiwa terjadi, atau seberapa besar kemungkinan suatu proposisi itu benar.
Untuk menyempurnakan teori ini, dapat di buka link dibawah ini dalam bentuk soal dan pembahasan
Peluang (Probabilitas) suatu peristiwa adalah angka antara 0 dan 1, di mana, secara kasar, 0 menunjukkan ketidakmungkinan peristiwa dan 1 menunjukkan kepastian. Semakin tinggi Peluang (Probabilitas) suatu peristiwa, semakin besar kemungkinan bahwa peristiwa itu akan terjadi. Contoh sederhana adalah pelemparan koin yang adil (tidak memihak). Karena koin itu adil, dua hasil ("kepala" dan "ekor") keduanya sama-sama mungkin; Peluang (Probabilitas) "kepala" sama dengan Peluang (Probabilitas) "ekor"; dan karena tidak ada hasil lain yang mungkin, Peluang (Probabilitas) "kepala" atau "ekor" adalah 1/2 (yang juga dapat ditulis sebagai 0,5 atau 50%).
Konsep-konsep ini telah diberikan formalisasi matematika aksiomatik dalam teori Peluang (Probabilitas), yang digunakan secara luas dalam bidang studi seperti statistik, matematika, sains, keuangan, perjudian, kecerdasan buatan, pembelajaran mesin, ilmu komputer, teori permainan, dan filsafat untuk, untuk contoh, menarik kesimpulan tentang frekuensi yang diharapkan dari peristiwa. Teori Peluang (Probabilitas) juga digunakan untuk menggambarkan mekanika dan keteraturan yang mendasari sistem yang kompleks.
Ketika berhadapan dengan eksperimen yang acak dan terdefinisi dengan baik dalam pengaturan teoretis murni (seperti melempar koin), Peluang (Probabilitas) dapat dijelaskan secara numerik dengan jumlah hasil yang diinginkan, dibagi dengan jumlah total semua hasil. Misalnya, melempar koin dua kali akan menghasilkan hasil "kepala-kepala", "kepala-ekor", "kepala-ekor", dan "ekor-ekor". Peluang (Probabilitas) mendapatkan hasil "kepala-kepala" adalah 1 dari 4 hasil, atau, dalam istilah numerik, 1/4, 0,25 atau 25%. Namun, ketika sampai pada aplikasi praktis, ada dua kategori utama interpretasi Peluang (Probabilitas) yang bersaing, yang penganutnya memiliki pandangan berbeda tentang sifat dasar Peluang (Probabilitas):
Objektivis menetapkan angka untuk menggambarkan beberapa keadaan objektif atau fisik. Versi Peluang (Probabilitas) objektif yang paling populer adalah Peluang (Probabilitas) frequentist, yang menyatakan bahwa Peluang (Probabilitas) peristiwa acak menunjukkan frekuensi relatif kemunculan hasil eksperimen ketika eksperimen diulang tanpa batas. Interpretasi ini menganggap Peluang (Probabilitas) sebagai frekuensi relatif "dalam jangka panjang" dari hasil. Modifikasi dari ini adalah Peluang (Probabilitas) kecenderungan, yang menafsirkan Peluang (Probabilitas) sebagai kecenderungan beberapa eksperimen untuk menghasilkan hasil tertentu, bahkan jika itu dilakukan hanya sekali.
Subjektivis menetapkan angka per Peluang (Probabilitas) subjektif, yaitu, sebagai tingkat kepercayaan. Tingkat kepercayaan telah ditafsirkan sebagai "harga di mana Anda akan membeli atau menjual taruhan yang membayar 1 unit utilitas jika E, 0 jika bukan E." Versi Peluang (Probabilitas) subjektif yang paling populer adalah Peluang (Probabilitas) Bayesian, yang mencakup pengetahuan ahli serta data eksperimen untuk menghasilkan Peluang (Probabilitas). Pengetahuan ahli diwakili oleh beberapa distribusi Peluang (Probabilitas) sebelumnya (subyektif). Data ini tergabung dalam fungsi kemungkinan. Produk dari prior dan kemungkinan, ketika dinormalisasi, menghasilkan distribusi Peluang (Probabilitas) posterior yang menggabungkan semua informasi yang diketahui hingga saat ini. Dengan teorema kesepakatan Aumann, agen Bayesian yang keyakinan sebelumnya serupa akan berakhir dengan keyakinan posterior serupa. Namun, prioritas yang cukup berbeda dapat menyebabkan kesimpulan yang berbeda, terlepas dari seberapa banyak informasi yang dibagikan oleh agen.
Peluang (Probabilitas) adalah kemungkinan atau peluang terjadinya suatu peristiwa.
Peluang (Probabilitas) = jumlah cara untuk mencapai keberhasilan / jumlah total hasil yang mungkin
Misalnya, peluang pelemparan koin dan menjadi kepala adalah , karena ada 1 cara untuk mendapatkan kepala dan jumlah hasil yang mungkin adalah 2 (kepala atau ekor). Kami menulis P(kepala) = .
Peluang sesuatu yang pasti terjadi adalah 1.
Peluang terjadinya sesuatu yang tidak mungkin terjadi adalah 0.
Peluang (Probabilitas) sesuatu yang tidak terjadi adalah 1 dikurangi Peluang (Probabilitas) bahwa hal itu akan terjadi.
Acara Tunggal
Contoh
Ada 6 manik-manik di dalam tas, 3 berwarna merah, 2 berwarna kuning dan 1 berwarna biru. Berapa peluang terambilnya kuning?
Peluangnya adalah jumlah kuning dalam kantong dibagi dengan jumlah bola, yaitu 2/6 = 1/3.
Contoh
Ada sebuah tas berisi bola-bola berwarna, merah, biru, hijau dan jingga. Bola diambil dan diganti. John melakukan ini 1000 kali dan memperoleh hasil sebagai berikut:
Jumlah bola biru yang terambil: 300
Jumlah bola merah: 200
Jumlah bola hijau: 450
Jumlah bola oranye: 50
a) Berapa peluang terambilnya bola hijau?
Untuk setiap 1000 bola yang diambil, 450 berwarna hijau. Oleh karena itu P(hijau) = 450/1000 = 0,45
b) Jika ada 100 bola di dalam kantong, berapa banyak bola yang kemungkinan berwarna hijau?
Percobaan menunjukkan bahwa 450 dari 1000 bola berwarna hijau. Oleh karena itu, dari 100 bola, 45 berwarna hijau (menggunakan rasio).
Beberapa Acara
Acara Independen dan Dependen
Misalkan sekarang kita mempertimbangkan Peluang (Probabilitas) 2 peristiwa terjadi. Misalnya, kita mungkin melempar 2 dadu dan mempertimbangkan Peluang (Probabilitas) bahwa keduanya adalah 6.
Kami menyebut dua peristiwa independen jika hasil dari salah satu peristiwa tidak mempengaruhi hasil yang lain. Sebagai contoh, jika kita melempar dua dadu, peluang munculnya angka 6 pada dadu kedua adalah sama, berapa pun yang kita peroleh dengan dadu pertama - tetap 1/6.
Di sisi lain, misalkan kita memiliki tas berisi 2 bola merah dan 2 bola biru. Jika kita mengambil 2 bola dari kantong, peluang terambilnya bola kedua berwarna biru tergantung pada warna bola pertama yang diambil. Jika bola pertama berwarna biru, akan ada 1 bola biru dan 2 bola merah di dalam kantong saat kita mengambil bola kedua. Jadi peluang terambilnya warna biru adalah 1/3. Akan tetapi, jika bola pertama berwarna merah, maka akan tersisa 1 bola merah dan 2 bola biru sehingga peluang terambilnya bola kedua berwarna biru adalah 2/3. Ketika Peluang (Probabilitas) satu peristiwa tergantung pada yang lain, peristiwa itu tergantung.
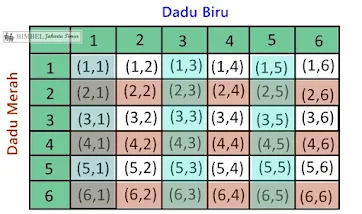
Ketika mencari tahu apa Peluang (Probabilitas) dari dua hal yang terjadi, ruang Peluang (Probabilitas)/kemungkinan dapat ditarik. Misalnya, jika Anda melempar dua dadu, berapa peluang Anda mendapatkan: a) 8, b) 9, c) 8 atau 9?
Kemungkinan
a) Gumpalan hitam menunjukkan cara mendapatkan 8 (a 2 dan a 6, a 3 dan a 5, ...). Ada 5 cara berbeda. Ruang peluang menunjukkan kepada kita bahwa ketika melempar 2 dadu, ada 36 kemungkinan yang berbeda (36 kotak). Dengan 5 dari kemungkinan ini, Anda akan mendapatkan 8. Oleh karena itu P(8) = 5/36 .
b) Gumpalan merah menunjukkan cara mendapatkan 9. Ada empat cara, oleh karena itu P(9) = 4/36 = 1/9.
c) Anda akan mendapatkan 8 atau 9 di salah satu kotak 'gumpalan'. Ada 9 semuanya, jadi P(8 atau 9) = 9/36 = 1/4 .
Pohon Peluang (Probabilitas)
Cara lain untuk merepresentasikan 2 atau lebih kejadian adalah pada pohon Peluang (Probabilitas).
Contoh
Dalam sebuah kantong terdapat 3 bola : merah, kuning, dan biru. Satu bola diambil, dan tidak diganti, dan kemudian bola lain diambil.
Pohon Peluang (Probabilitas)
Bola pertama bisa berwarna merah, kuning atau biru. Peluang (Probabilitas)nya adalah 1/3 untuk masing-masing. Jika diambil bola merah, maka akan tersisa dua bola, kuning dan biru. Peluang terambilnya bola kedua berwarna kuning adalah 1/2 dan peluang terambilnya bola kedua berwarna biru adalah 1/2. Logika yang sama dapat diterapkan pada kasus-kasus ketika bola kuning atau biru diambil terlebih dahulu.
Dalam contoh ini, pertanyaannya menyatakan bahwa bola tidak diganti. Jika ya, peluang terambilnya bola merah (dst.) untuk kedua kalinya akan sama dengan yang pertama (yaitu 1/3).
Aturan AND dan OR (Tingkat TINGGI)
Dalam contoh di atas, peluang terambilnya yang pertama berwarna merah adalah 1/3 dan yang kedua berwarna kuning adalah 1/2. Peluang terambilnya sebuah AND merah kemudian kuning adalah 1/3 × 1/2 = 1/6 (ini ditunjukkan di ujung cabang). Aturannya adalah:
Jika dua peristiwa A dan B saling bebas (ini berarti bahwa satu peristiwa tidak bergantung pada yang lain), maka peluang terjadinya A dan B ditemukan dengan mengalikan peluang terjadinya A dengan peluang terjadinya B.
Peluang terambilnya warna merah ATAU kuning terlebih dahulu adalah 1/3 + 1/3 = 2/3. Aturannya adalah:
Jika terdapat dua kejadian A dan B dan kedua kejadian tersebut tidak mungkin terjadi, maka peluang terjadinya A atau B adalah peluang terjadinya A + peluang terjadinya B.
Pada pohon Peluang (Probabilitas), ketika bergerak dari kiri ke kanan kita mengalikan dan ketika bergerak ke bawah kita menjumlahkan.
Contoh
Berapakah peluang terambilnya kuning dan merah pada sembarang urutan?
Ini sama dengan: berapa peluang terambilnya kuning DAN merah ATAU merah DAN kuning.
P(kuning dan merah) = 1/3 × 1/2 = 1/6
P(merah dan kuning) = 1/3 × 1/2 = 1/6
P(kuning dan merah atau merah dan kuning) = 1/6 + 1/6 = 1/3
Kemungkinan
Peluang (Probabilitas) mendefinisikan kemungkinan terjadinya suatu peristiwa. Ada banyak situasi kehidupan nyata di mana kita mungkin harus memprediksi hasil dari suatu peristiwa. Kita mungkin yakin atau tidak yakin dengan hasil suatu peristiwa. Dalam kasus seperti itu, kami mengatakan bahwa ada kemungkinan peristiwa ini terjadi atau tidak terjadi. Peluang (Probabilitas) umumnya memiliki aplikasi yang hebat dalam permainan, dalam bisnis untuk membuat prediksi berbasis Peluang (Probabilitas), dan juga Peluang (Probabilitas) memiliki aplikasi yang luas di bidang kecerdasan buatan yang baru ini.
Peluang (Probabilitas) suatu peristiwa dapat dihitung dengan rumus Peluang (Probabilitas) dengan hanya membagi jumlah hasil yang diinginkan dengan jumlah total hasil yang mungkin. Nilai peluang suatu peristiwa untuk terjadi dapat terletak antara 0 dan 1 karena jumlah hasil yang diinginkan tidak pernah dapat melampaui jumlah total hasil. Juga, jumlah hasil yang menguntungkan tidak boleh negatif. Mari kita bahas dasar-dasar Peluang (Probabilitas) secara rinci di bagian berikut.
Apa itu Peluang (Probabilitas)?
Peluang (Probabilitas) dapat didefinisikan sebagai rasio jumlah hasil yang menguntungkan dengan jumlah total hasil dari suatu peristiwa. Untuk eksperimen yang memiliki jumlah hasil 'n', jumlah hasil yang disukai dapat dilambangkan dengan x. Rumus untuk menghitung peluang suatu kejadian adalah sebagai berikut.
Peluang (Probabilitas)(Peristiwa) = Hasil yang Menguntungkan/Total Hasil = x/n
Mari kita periksa aplikasi sederhana dari Peluang (Probabilitas) untuk memahaminya dengan lebih baik. Misalkan kita harus memprediksi tentang terjadinya hujan atau tidak. Jawaban atas pertanyaan ini adalah "Ya" atau "Tidak". Ada kemungkinan hujan atau tidak hujan. Di sini kita dapat menerapkan Peluang (Probabilitas). Peluang (Probabilitas) digunakan untuk memprediksi hasil dari pelemparan koin, pelemparan dadu, atau pengambilan kartu dari paket kartu remi.
Peluang (Probabilitas) diklasifikasikan menjadi Peluang (Probabilitas) teoritis dan Peluang (Probabilitas) eksperimental.
Terminologi Teori Peluang (Probabilitas)
Istilah-istilah berikut dalam Peluang (Probabilitas) membantu dalam pemahaman yang lebih baik tentang konsep-konsep Peluang (Probabilitas).
Percobaan: Percobaan atau operasi yang dilakukan untuk menghasilkan suatu hasil disebut percobaan.
Ruang Sampel: Semua hasil yang mungkin dari suatu percobaan bersama-sama membentuk ruang sampel. Misalnya, ruang sampel pelemparan uang logam adalah kepala dan ekor.
Hasil yang Menguntungkan: Suatu peristiwa yang telah menghasilkan hasil yang diinginkan atau peristiwa yang diharapkan disebut hasil yang menguntungkan. Misalnya, ketika kita melempar dua dadu, hasil yang mungkin/menguntungkan untuk mendapatkan jumlah angka pada kedua dadu adalah 4 adalah (1,3), (2,2), dan (3,1).
Percobaan: Percobaan menunjukkan melakukan percobaan acak.
Eksperimen Acak: Eksperimen yang memiliki serangkaian hasil yang ditentukan dengan baik disebut eksperimen acak. Misalnya, ketika kita melempar koin, kita tahu bahwa kita akan maju atau mundur, tetapi kita tidak yakin mana yang akan muncul.
Peristiwa: Jumlah total hasil percobaan acak disebut peristiwa.
Kemungkinan Kejadian yang Sama: Kejadian yang memiliki peluang atau peluang yang sama untuk terjadi disebut kejadian yang sama kemungkinannya. Hasil dari satu peristiwa tidak tergantung pada yang lain. Misalnya, ketika kita melempar koin, ada peluang yang sama untuk mendapatkan kepala atau ekor.
Peristiwa Lengkap: Ketika himpunan semua hasil percobaan sama dengan ruang sampel, kita menyebutnya peristiwa lengkap.
Peristiwa Saling Eksklusif: Peristiwa yang tidak dapat terjadi secara bersamaan disebut peristiwa saling lepas. Misalnya, iklim bisa panas atau dingin. Kita tidak bisa mengalami cuaca yang sama secara bersamaan.
Rumus Peluang (Probabilitas)
Rumus Peluang (Probabilitas) mendefinisikan kemungkinan terjadinya suatu peristiwa. Ini adalah rasio hasil yang menguntungkan dengan total hasil yang menguntungkan. Rumus Peluang (Probabilitas) dapat dinyatakan sebagai,
P(A)=jumlah hasil yang menguntungkan ke A / jumlah total hasil yang mungkin
di mana,
P(B) adalah peluang suatu kejadian 'B'.
n(B) adalah jumlah hasil yang menguntungkan dari suatu peristiwa 'B'.
n(S) adalah jumlah total kejadian yang terjadi dalam ruang sampel.
Rumus Peluang (Probabilitas) Berbeda
Rumus peluang dengan aturan penjumlahan: Setiap kali suatu peristiwa adalah gabungan dari dua peristiwa lainnya, katakanlah A dan B, maka
P(A atau B) = P(A) + P(B) - P(A∩B)
P(A B) = P(A) + P(B) - P(A∩B)
Rumus peluang dengan aturan komplementer: Setiap kali suatu peristiwa adalah pelengkap dari peristiwa lain, khususnya, jika A adalah suatu peristiwa, maka P(bukan A) = 1 - P(A) atau P(A') = 1 - P(A ).
P(A) + P(A′) = 1.
Rumus peluang dengan aturan bersyarat: Ketika peristiwa A telah diketahui telah terjadi dan peluang peristiwa B diinginkan, maka P(B, diberikan A) = P(A dan B), P(A, diberikan B). Hal ini dapat terjadi sebaliknya dalam kasus kejadian B.
P(B∣A) = P(A∩B)/P(A)
Rumus peluang dengan aturan perkalian: Setiap kali suatu peristiwa merupakan perpotongan dari dua peristiwa lain, yaitu peristiwa A dan B harus terjadi secara bersamaan. Maka P(A dan B) = P(A)⋅P(B).
P(A∩B) = P(A)⋅P(B∣A)
Contoh 1: Temukan peluang munculnya angka kurang dari 5 ketika sebuah dadu dilempar dengan menggunakan rumus peluang.
Soal
Mencari:Peluang muncul angka kurang dari 5
Diketahui: Ruang sampel = {1,2,3,4,5,6}
Mendapatkan angka kurang dari 5 = {1,2,3,4}
Oleh karena itu, n(S) = 6
n(A) = 4
Menggunakan Rumus Peluang (Probabilitas),
P(A) = (n(A))/(n(s))
p(A) = 4/6
m = 2/3
Jawaban: Peluang muncul angka kurang dari 5 adalah 2/3.
Contoh 2: Berapa peluang munculnya jumlah 9 ketika dua buah dadu dilempar?
Soal:
Ada total 36 kemungkinan ketika kita melempar dua dadu.
Untuk mendapatkan hasil yang diinginkan yaitu, 9, kita dapat memiliki hasil yang menguntungkan berikut.
(4,5),(5,4),(6,3)(3,6). Ada 4 hasil yang menguntungkan.
Peluang suatu kejadian P(E) = (Jumlah hasil yang menguntungkan) (Total hasil dalam ruang sampel)
Peluang muncul angka 9 = 4 36 = 1/9
Jawab: Jadi peluang munculnya jumlah 9 adalah 1/9.
Diagram Pohon Peluang (Probabilitas)
Diagram pohon dalam Peluang (Probabilitas) adalah representasi visual yang membantu dalam menemukan hasil yang mungkin atau Peluang (Probabilitas) suatu peristiwa terjadi atau tidak terjadi. Diagram pohon untuk lemparan koin yang diberikan di bawah ini membantu dalam memahami kemungkinan hasil ketika sebuah koin dilempar dan dengan demikian dalam menemukan Peluang (Probabilitas) mendapatkan kepala atau ekor ketika sebuah koin dilempar.
Jenis Peluang (Probabilitas)
Mungkin ada perspektif atau jenis Peluang (Probabilitas) yang berbeda berdasarkan pada sifat hasil atau pendekatan yang diikuti saat menemukan kemungkinan suatu peristiwa terjadi. Empat jenis peluang tersebut adalah,
- Peluang (Probabilitas) Klasik
- Peluang (Probabilitas) Empiris
- Peluang (Probabilitas) Subyektif
- Peluang (Probabilitas) Aksiomatik
Peluang (Probabilitas) Klasik
Peluang (Probabilitas) klasik, sering disebut sebagai "priori" atau "Peluang (Probabilitas) teoretis", menyatakan bahwa dalam sebuah eksperimen di mana ada B hasil yang kemungkinannya sama, dan kejadian X memiliki tepat A dari hasil ini, maka Peluang (Probabilitas) X adalah A/B, atau P(X) = A/B. Misalnya, ketika dadu yang adil dilempar, ada enam kemungkinan hasil yang sama-sama mungkin. Artinya, ada peluang 1/6 untuk melempar setiap angka pada dadu.
Peluang (Probabilitas) Empiris
Peluang (Probabilitas) empiris atau perspektif eksperimental mengevaluasi Peluang (Probabilitas) melalui eksperimen pemikiran. Misalnya, jika sebuah dadu berbobot dilempar, sehingga kita tidak tahu sisi mana yang memiliki bobot, maka kita bisa mendapatkan ide untuk Peluang (Probabilitas) setiap hasil dengan menggulung dadu beberapa kali dan menghitung proporsi kali dadu memberikan hasil itu dan dengan demikian menemukan Peluang (Probabilitas) hasil itu.
Peluang (Probabilitas) Subyektif
Peluang (Probabilitas) subyektif mempertimbangkan keyakinan individu tentang suatu peristiwa yang terjadi. Misalnya, kemungkinan tim tertentu memenangkan pertandingan sepak bola berdasarkan pendapat penggemar lebih bergantung pada keyakinan dan perasaan mereka sendiri dan bukan pada perhitungan matematis formal.
Peluang (Probabilitas) Aksiomatik
Dalam Peluang (Probabilitas) aksiomatik, seperangkat aturan atau aksioma oleh Kolmogorov diterapkan pada semua tipe. Peluang terjadinya atau tidak terjadinya suatu peristiwa dapat diukur dengan penerapan aksioma-aksioma ini, diberikan sebagai,
Peluang (Probabilitas) terkecil yang mungkin adalah nol, dan yang terbesar adalah satu.
Suatu kejadian yang pasti mempunyai peluang sama dengan satu.
Dua peristiwa yang saling eksklusif tidak dapat terjadi secara bersamaan, sedangkan penyatuan peristiwa mengatakan hanya satu dari mereka yang dapat terjadi.
Mencari Peluang Suatu Kejadian
Dalam suatu eksperimen, peluang suatu peristiwa adalah kemungkinan terjadinya peristiwa itu. Peluang (Probabilitas) dari setiap peristiwa adalah nilai antara (dan termasuk) "0" dan "1".
Peristiwa dalam Peluang (Probabilitas)
Dalam teori Peluang (Probabilitas), suatu peristiwa adalah himpunan hasil dari suatu eksperimen atau himpunan bagian dari ruang sampel.
Jika P(E) menyatakan peluang suatu kejadian E, maka, kita memiliki,
P(E) = 0 jika dan hanya jika E adalah kejadian yang tidak mungkin.
P(E) = 1 jika dan hanya jika E adalah kejadian tertentu.
0 P(E) 1.
Misalkan, kita diberi dua kejadian, "A" dan "B", maka peluang kejadian A, P(A) > P(B) jika dan hanya jika kejadian "A" lebih mungkin terjadi daripada kejadian "B ". Ruang sampel(S) adalah himpunan semua hasil yang mungkin dari suatu percobaan dan n(S) menyatakan jumlah hasil dalam ruang sampel.
P(E) = n(E)/n(S)
P(E’) = (n(S) - n(E))/n(S) = 1 - (n(E)/n(S))
E’ menyatakan bahwa peristiwa itu tidak akan terjadi.
Oleh karena itu, sekarang kita juga dapat menyimpulkan bahwa, P(E) + P(E’) = 1
Peluang Lemparan Koin
Sekarang mari kita lihat peluang pelemparan koin. Cukup sering dalam permainan seperti kriket, untuk membuat keputusan siapa yang akan bermain bowling atau bat lebih dulu, terkadang kita menggunakan lemparan koin dan memutuskan berdasarkan hasil lemparan. Mari kita periksa bagaimana kita dapat menggunakan konsep Peluang (Probabilitas) dalam pelemparan satu koin. Selanjutnya, kita juga akan melihat pelemparan dua dan tiga yang datang masing-masing.
Melempar Koin
Satu koin pada pelemparan memiliki dua hasil, kepala, dan ekor. Konsep Peluang (Probabilitas) yang merupakan rasio hasil yang menguntungkan dengan jumlah total hasil dapat digunakan untuk menemukan Peluang (Probabilitas) mendapatkan kepala dan Peluang (Probabilitas) mendapatkan ekor.
Jumlah total hasil yang mungkin = 2; Ruang Sampel = {H, T}; H: Kepala, T: Ekor
P(H) = Jumlah kepala/Total hasil = 1/2
P(T)= Jumlah Ekor/ Total hasil = 1/2
Melempar Dua Koin
Dalam proses melempar dua koin, kami memiliki total empat hasil. Rumus Peluang (Probabilitas) dapat digunakan untuk menemukan Peluang (Probabilitas) dua kepala, satu kepala, tidak ada kepala, dan Peluang (Probabilitas) serupa dapat dihitung untuk jumlah ekor. Perhitungan Peluang (Probabilitas) untuk dua kepala adalah sebagai berikut.
Jumlah hasil = 4; Ruang Sampel = {(H, H), (H, T), (T, H), (T, T)}
P(2H) = P(0 T) = Jumlah hasil dengan dua kepala/Total Hasil = 1/4
P(1H) = P(1T) = Jumlah hasil dengan hanya satu kepala/Total Hasil = 2/4 = 1/2
P(0H) = (2T) = Jumlah hasil dengan dua kepala/Total Hasil = 1/4
Melempar Tiga Koin
Banyaknya hasil total pelemparan tiga uang logam secara bersamaan sama dengan 23 = 8. Untuk hasil tersebut, kita dapat menemukan peluang muncul satu kepala, dua kepala, tiga kepala, dan tidak ada kepala. Peluang (Probabilitas) serupa juga dapat dihitung untuk jumlah ekor.
Jumlah hasil = 23 = 8 Ruang Sampel = {(H, H, H), (H, H, T), (H, T, H), (T, H, H), (T, T, H ), (T, H, T), (H, T, T), (T, T, T)}
P(0H) = P(3T) = Jumlah hasil tanpa kepala/Total Hasil = 1/8
P(1H) = P(2T) = Jumlah Hasil dengan satu kepala/Total Hasil = 3/8
P(2H) = P(1T) = Jumlah hasil dengan dua kepala /Total Hasil = 3/8
P(3H) = P(0T) = Jumlah hasil dengan tiga kepala/Total Hasil = 1/8
Peluang (Probabilitas) Pelemparan Dadu
Banyak permainan menggunakan dadu untuk memutuskan gerakan pemain di seluruh permainan. Sebuah dadu memiliki enam kemungkinan hasil dan hasil dari sebuah dadu adalah permainan peluang dan dapat diperoleh dengan menggunakan konsep peluang. Beberapa permainan juga menggunakan dua dadu, dan ada banyak peluang yang dapat dihitung untuk hasil menggunakan dua dadu. Sekarang mari kita periksa hasilnya, peluangnya untuk masing-masing satu dadu dan dua dadu.
Melempar Satu Dadu
Banyaknya hasil pelemparan sebuah dadu adalah 6, dan ruang sampelnya adalah {1, 2, 3, 4, 5, 6}. Di sini kita akan menghitung beberapa Peluang (Probabilitas) berikut untuk membantu dalam pemahaman yang lebih baik tentang konsep Peluang (Probabilitas) pada pelemparan satu dadu.
P(Bilangan Genap) = Banyaknya hasil bilangan genap/Total Hasil = 3/6 = 1/2
P(Bilangan Ganjil) = Banyaknya hasil bilangan ganjil/Total Hasil = 3/6 = 1/2
P(Bilangan Prima) = Jumlah hasil bilangan prima/Total Hasil = 3/6 = 1/2
Melempar Dua Dadu
Banyaknya hasil pelemparan dua buah dadu adalah 62 = 36. Gambar berikut menunjukkan ruang sampel dari 36 hasil pelemparan dua buah dadu.
Mari kita periksa beberapa Peluang (Probabilitas) hasil dari dua dadu. Peluang (Probabilitas)nya adalah sebagai berikut.
Peluang mendapatkan doublet(Bilangan yang sama) = 6/36 = 1/6
Peluang terambilnya angka 3 pada paling sedikit satu dadu = 11/36
Peluang muncul jumlah 7 = 6/36 = 1/6
Seperti yang kita lihat, ketika kita melempar satu dadu, ada 6 kemungkinan. Ketika kita melempar dua dadu, ada 36 kemungkinan. Ketika kita melempar 3 dadu, kita mendapatkan 216 kemungkinan. Jadi rumus umum untuk menyatakan banyaknya hasil pada pelemparan dadu 'n' adalah 6n.
Peluang (Probabilitas) gambar Kartu
Dek yang berisi 52 kartu dikelompokkan menjadi empat setelan tongkat, berlian, hati, dan sekop. Masing-masing gada, berlian, hati, dan sekop masing-masing memiliki 13 kartu, yang berjumlah 52. Sekarang mari kita bahas peluang terambilnya kartu dari satu pak. Simbol pada kartu ditunjukkan di bawah ini. Sekop dan tongkat adalah kartu hitam. Hati dan berlian adalah kartu merah.
13 kartu di setiap suit adalah ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen, king. Dalam hal ini, jack, ratu, dan raja disebut kartu wajah. Kita dapat memahami peluang kartu dari contoh berikut.
Peluang terambilnya kartu hitam adalah P(Kartu hitam) = 26/52 = 1/2
Peluang terambilnya kartu hati adalah P(Hati) = 13/52 = 1/4
Peluang terambilnya kartu bergambar adalah P(Kartu muka) = 12/52 = 3/13
Peluang terambilnya kartu bernomor 4 adalah P(4) = 4/52 = 1/13
Peluang terambilnya kartu merah bernomor 4 adalah P(4 Merah) = 2/52 = 1/26
Teorema Peluang (Probabilitas)
Teorema Peluang (Probabilitas) berikut sangat membantu untuk memahami penerapan Peluang (Probabilitas) dan juga melakukan banyak perhitungan yang melibatkan Peluang (Probabilitas).
Teorema 1: Jumlah peluang terjadinya suatu peristiwa dan tidak terjadinya suatu peristiwa sama dengan 1.
P(A)+P(¯A)=1
Teorema 2: Peluang (Probabilitas) suatu kejadian yang tidak mungkin atau Peluang (Probabilitas) suatu kejadian yang tidak terjadi selalu sama dengan 0.
P(ϕ)=0
Teorema 3: Peluang (Probabilitas) suatu kejadian pasti selalu sama dengan 1. P(A) = 1
Teorema 4: Peluang (Probabilitas) terjadinya suatu peristiwa selalu terletak antara 0 dan 1. 0 < P(A) < 1
Teorema 5: Jika ada dua kejadian A dan B, kita dapat menerapkan rumus gabungan dua himpunan dan kita dapat menurunkan rumus peluang terjadinya kejadian A atau kejadian B sebagai berikut.
P(A∪B)=P(A)+P(B)−P(A∩B)
Juga untuk dua kejadian yang saling lepas A dan B, kita memiliki P( A U B) = P(A) + P(B)
Teorema Bayes tentang Peluang Bersyarat
Teorema Bayes menggambarkan Peluang (Probabilitas) suatu peristiwa berdasarkan kondisi terjadinya peristiwa lain. Ini juga disebut Peluang (Probabilitas) bersyarat. Ini membantu dalam menghitung Peluang (Probabilitas) terjadinya satu peristiwa berdasarkan kondisi terjadinya peristiwa lain.
Sebagai contoh, mari kita asumsikan bahwa ada tiga kantong dengan masing-masing kantong berisi beberapa bola biru, hijau, dan kuning. Berapa peluang terambilnya bola kuning dari kantong ketiga? Karena ada bola berwarna biru dan hijau juga, kita dapat sampai pada Peluang (Probabilitas) berdasarkan kondisi ini juga. Peluang (Probabilitas) seperti itu disebut Peluang (Probabilitas) bersyarat.
Rumus untuk teorema Bayes adalah
P(A|B)=P(B|A)⋅P(A)P(B) dimana,
P(A|B) menunjukkan seberapa sering kejadian A terjadi dengan syarat B terjadi.
dimana, P(B|A)
menunjukkan seberapa sering peristiwa B terjadi pada kondisi bahwa A terjadi.
P(A) peluang terjadinya kejadian A.
P(B) peluang terjadinya kejadian B.
Hukum Peluang (Probabilitas) Total
Jika ada n kejadian dalam suatu percobaan, maka jumlah peluang dari n kejadian tersebut selalu sama dengan 1.
P(A1)+P(A2)+P(A3)+....P(An)=1
Tag.
rumus peluang kejadian majemuk
peluang statistika
peluang adalah
peluang kejadian bersyarat
jenis-jenis peluang matematika
materi peluang smp
materi peluang pdf
materi peluang kuliah
cara menghitung probabilitas
probabilitas statistika adalah
contoh soal probabilitas statistika dan penyelesaiannya
probabilitas pdf
aturan probabilitas
ilmu dan probabilitas
contoh probabilitas
statistika dan probabilitas teknik sipil
materi peluang kelas 12
peluang statistika
peluang matematika
peluang dua dadu
peluang dadu
materi peluang smp
rumus peluang statistika
peluang empirik
contoh soal peluang dan pembahasannya pdf
soal peluang kelas 12
contoh soal peluang dan pembahasannya kelas 12
contoh soal peluang kelas 8
contoh soal peluang untuk mahasiswa
contoh soal peluang dan jawabannya
contoh soal peluang dan pembahasannya brainly
contoh soal peluang kelereng dan pembahasannya


 Scholar Bimbel Jakarta Timur, Bimbel Matematika IPA, Fisika Kimia Biologi, SD SMP SMA, IT Training, di Jakarta Timur No. Hp: 082210027724
Scholar Bimbel Jakarta Timur, Bimbel Matematika IPA, Fisika Kimia Biologi, SD SMP SMA, IT Training, di Jakarta Timur No. Hp: 082210027724



















0 Komentar